Background

Leetcode and DSA.

Great pain.

I’ve been doing this for quite long, but I’d like to improve my intuition. My general feel is that leetcode is getting a lot less important as Claude Code and other tools become more robust. Which is both good and bad.

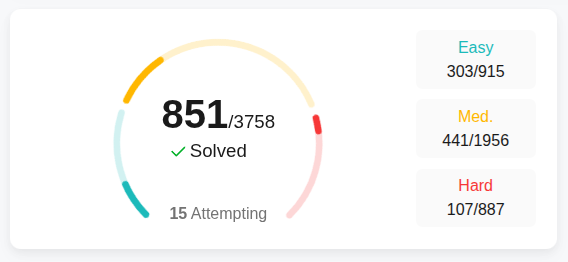
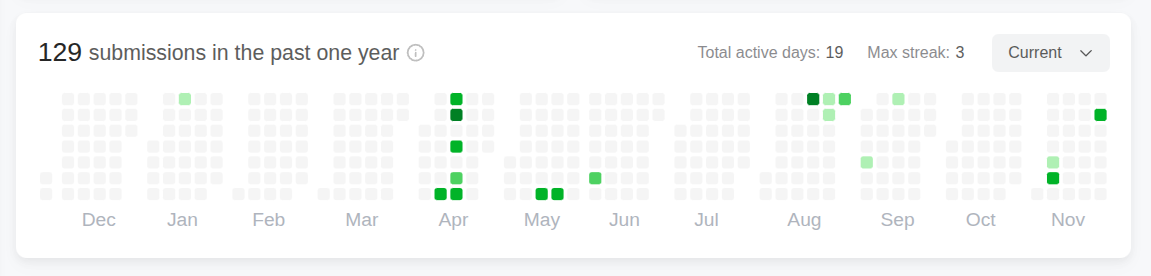
I’ve done quite a lot of leetcode in the past, but none recently. Previously when I learned how to do leetcode with Python, I found it useful to do a lot of easy problems to remind myself of the syntax. Some of these snippets are from leetcode, some of it is from other sources, some of them I made up.

I’m going to write this in Python, and mayyybe I’ll come back and do it in C++. Probably not. I’m going to treat this page as the dumping ground for the first 150, standard problems. This is probably quite a boring page, unfortunately.

Practice Philosophy

My rough belief is there’s a large set of knowledge sets or tricks which are a prerequisites to doing a given problem. If we don’t know the trick at all, it’s going to take us unreasonably long to solve the problem, or we won’t solve it at all. If we roughly know the trick, and we can implement it, then we can solve it in a reasonable amount of time. Finally, if we deeply know the trick, how to explain the trick, and how to implement the trick, then we can solve problems fluently. How we practice should be optimised for around this.

Are we doing codeforces problems? Then we should roughly know a range of tricks and practice figuring out the solution from there. We should know how to do common patterns quickly, but that’s fast to learn, then we should roughly know a very wide range of patterns, and practice being able to implement obscure problems from that tool bag. This way, you can improve your intuition and reasoning over time, and accelerate it from the patterns you know. However, we wouldn’t need to optimise explaining the problem at all.

If we’re interviewing, we should almost always hope our questions fall in the third category. We need to prioritise explaining to people. Unless someone just handed you a segment-tree tier question, we should not take long to go from thinking to explaining it to them. Having your interviewer wait for two minutes while you think in silence is a bad signal. At least it’s better than rambling in circles for ten minutes, though.

This framework breaks learning into three types. Learning the initial topic, practicing problems with the topic, and practicing explaining the topic. The best is a balance and it isn’t worth over-specialising for our goal. I’ll begin by revising the basics with grind 75, making sure I’m confident at them, can explain them well (practiced by writing), then move into learning new topics and practicing those topics until they’re at the edge of my ELO.

There are also other things I need to learn - system trivia (AIGC, compilers, databases, message queues, language features), and system design at some point. So I won’t be doing this infinitely.

Syntax

List syntax

# Say you have some list
items = [5, 4, 3, 2, 1]
 
# This builds a list list [(1, 0), (2, 0), ...]
indexed = [(x, i) for i, x in enumerate(items)] 
 
# This sort can be a bit slow because it needs to do a copy
sorted_indexed = sorted(indexed)
 
# This is inplace, but ruins the original 
indexed.sort()
 
# You can also filter while doing list comprehension
no_three = [x for x in items if x != 3]
evens = [x for x in items if x % 2 == 0]
 
# Slicing is pretty straight forwards. The start is inclusive, the end is exclusive
sliced = items[1:3] # [4, 3]
sliced = items[:2] # [5, 4]
sliced = items[-1] # the last element
sliced = items[::2] # 2nd element. I don't use this. Hard to read.
sliced = items[::-1] # Reversed. Again, I don't use this.
 
# Unpacking - this is a cool idea, but it costs O(n). so. doesn't make sense to use, most of the time.
first, *rest = items
first, *middle, last = items
 
# Functions
items.append(6)
items.extend([7, 8])
items.insert(0, 9) # insert 9 at index 0
last = items.pop() 
items.pop(0) # at index
items.remove(3) # removes the first three
first_idx = items.index(3) # index of the first 3, O(n)
freq = items.count(3) # how many 3s
items.clear()
items = [5, 4, 3, 2, 1] # reset it...
cpy = items.copy()
 
# inplace reverse
items.reverse()
items = list(reversed(items)) # copy reverse
 
total = sum(items)
min_val, max_val = min(items), max(items)
three_exists = any(x == 3 for x in items)
everything_positive = all(x >= 0 for x in items)
 
# zipping
names = [str(x) for x in items]
for name, val in zip(names, items):
    print(name, val)
    
# There's also map and filter functions, but list comprehension is preferred
val = list(filter(lambda x: x > 2, items))
val = list(map, lambda x: x * 2, items)
# can probably tell why since those are kinda gross
 
from functools import reduce
 
nums = [1, 2, 3, 4]
# the first argument is the accumulator
# I recommend using the naming `acc` and `cur` inside the 
# lambda to make this absolutely clear
total = reduce(lambda acc, cur: acc + cur, nums)
maxv = reduce(lambda acc, cur: acc if acc > cur else cur, nums)
 
# You can pass in an initialiser
# this will add in 10
total = reduce(lambda acc, cur: acc + cur, nums, 10)
# for a right fold you should just reverse the list
 
from functools import product
# this tool lets you iterate in 2D in one line
 
list1 = [1, 2, 3]
list2 = [4, 5, 6]
total = []
for a, b in product(list1, list2):
    total.append(a, b)
 
# this is equivalent to doing:
total = []
for a in list1:
    for b in list2:
        total.append(a, b)
 
# This can be particularly useful when you're reducing or using any() or all()
EMPTY, ROTTING, HEALTHY = 0, 1, 2
R, L = 3, 3
rotting_oranges = [[0, 1, 2], [0, 1, 2], [0, 1, 2]]
 
is_all_healthy = all(y == HEALTHY for _, y in product(range(R), range(L)))
is_any_healthy = any(y == HEALTHY for _, y in product(range(R), range(L)))
 
# or you could explode the list
flat = [cell for row in rotting_oranges for cell in row]
is_all_healthy = all(x == HEALTHY for x in flat)

Common string sets

import string
 
# Letters
string.ascii_letters        # 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ'
string.ascii_lowercase      # 'abcdefghijklmnopqrstuvwxyz'
string.ascii_uppercase      # 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
 
# Digits
string.digits               # '0123456789'
 
# Alphanumeric (combine letters + digits)
string.ascii_letters + string.digits
 
# Punctuation
string.punctuation          # '!"#$%&\'()*+,-./:;<=>?@[\\]^_`{|}~'
 
# Whitespace
string.whitespace           # ' \t\n\r\x0b\x0c'
 
# Everything printable
string.printable            # letters + digits + punctuation + whitespace

Strings

s = 'example string' # I think pep8 says single quotes are better
 
s2 = s + ' foo' # O(n + m), strings are immutable
 
# usually you'll want to do a join style thing with strings
s3 = " ".join(['one', 'two', 'three'])
 
# splitting
spl = s.split(' ')
s = s.split('e')
s = s.split()
 
s.replace('o', '0')
 
# Finds first index
# this is preferable to .index, because .index will throw an error
# if the item doesn't exist
# find just returns -1
f = s.find('e')
 
lowercase = s.lower()
uppercase = s.upper()
stripped = s.strip()
 
counts = s.count('e')
 
# strings are also kinda just lists so, you can do most of the list tricks above
# I won't dive into it
 
formatted = f'this is a {s} formatted string' 
 
# Reversing is a pain, if you reverse using reversed() it'll 
# return an iterator, and if you turn this iterator into a string
# it'll log like '<reversed object at 0x7f1231f5c250>' hahaha
# so you can use the [::-1] trick
reverse_string = formatted[::-1]
# maybe that's good in the future as well because it keeps it a list...
 
# You can left and right pad using rjust and ljust
# you can remember this as 'justify' in text alignment
v = "hhh"
a = v.rjust(5, '0') # hhh00
b = v.ljust(5, '0') # 00hhh

Counters

# Usually this isn't necessary
from collections import Counter
 
items = list(range(10))
count = Counter(items)
 
# 2nd most common element
mc = count.most_common(2)
# O(n log k), but n is the index you're looking for. it maintains a heap and pops the stuff out
 
# adds these numbers in 
count.update([5, 5, 1])
count += Counter([5, 5, 1])
 
# Be careful though, if you do this it duplicates the counter
# and wastes a bunch of space
count = count + Counter([5, 5, 1])
 
# Counts can intersect and union too
c1 = count1 & count2 # intersect; takes the minimum counts of the groups
c2 = count1 | count2 # maximum counts of the groups

Deques

# double ended queues are just lists
# but their left and right operations are O(1)
# and from my experimentation, it seems access via []
# is basically instant, but apparently the time complexity
# is O(k)
from collections import deque
items = deque(list(range(1000)))
items2 = deque([1, 2, 3])
left = items.popleft()
right = items.pop()
items.append(5)
items.appendleft(6)
 
# O(k) time complexity where k is the number of list 
# chunks in the deque
x = items[500] 
# >>> timeit.timeit(lambda: v[int(1e7)//2], number=int(1e4))
# 2.7693741470000077
# >>> timeit.timeit(lambda: v[0], number=int(1e4))
# 0.0007202019999681397
 
# about 4000 times slower to access the middle element in a 1e7 long deque

Dictionaries

d = {5: 'five', 4: 'four', 3: 'three'}
d = {}
 
five = d[5]
d[6] = 'six'
 
del d[5]
val = d.pop(4) # returns it, then pops it out
 
# get with a default
val = d.get(7, 'not found')
val = d.pop(4, 'not found')
 
d.keys()
d.values()
d.items()
 
# checks if its in the .keys(), useful for iterating
exist = 5 in d
 
d.update({6: 'six', 7: 'seven'})
d.clear()

Default dictionaries

# Default dictionaries confused me really hard when I was coming from python
# particularly that if you touch them, it inserts the element
 
# This isn't always necessary
from collections import defaultdict
 
counts = defaultdict(int)
words = defaultdict(list)
 
# the big thing is that you don't need to insert
# updating a value inserts the default value, then updates it
counts[5] += 1
 
# If you feel like dodging the insert, you can get
counts.get(5, 0)
 
# only sets the key if its missing
counts.setdefault(5, 0)

Heaps

# I heard there's a new min heap or max heap in python 3.14 or so
# but that's so new, I'm just going to ignore it
from heapq import * # not always necessary
 
items = [5, 4, 3, 2, 1]
heapify(items) # O(n)
 
heappush(items, 0)
x = heappop(items)
peek = items[0]
 
# you can use negatives to make a max heap
# if you want a lambda but remember your keys, use a tuple and put a 
# custom value at the front
# also nlargest is pretty cool, here's a solution for kClosest
class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        form = lambda x, y: x**2 + y**2
        dist = [(form(x, y), (x, y)) for x, y in points]
        return [(x, y) for _, (x, y) in nsmallest(k, dist)]

Tries

# There are two approach for tries, the original way or the 
# defaultdict trick.
# Inside an interview it depends on the context for which to use
 
class Trie:
    def __init__(self, letter):
        self.letter = letter
        self.children = {} # can be a default dict or a list
        self.end = False
    
    def insert(self, word):
        cur = self
        for c in word:
            if c not in cur.children:
                cur[c] = Trie(c)
            cur = cur[c]
        cur.end = True
 
    def find(self, word):
        cur = self
        for c in word:
            if c not in cur.children:
                return False
            cur = cur[c]
        return cur.end # you can return True for prefixes
        
        
# the default dict tree cuts out a lot of that
 
class Trie:
    def __init__(self, letter):
        def make_trie():
            return defaultdict(Trie)
        self.trie = make_trie()
    
    def insert(self, word):
        cur = self.trie
        for c in word:
            cur = cur[c]
        # This marks the end; you can also attach more information 
        # by using unused symbols, just making this True into a struct
        cur['#'] = True
 
    def find(self, word):
        cur = self.trie
        for c in word:
            if c not in cur:
                return False
            cur = cur[c]
        return '#' in cur
 
# You don't really need the class wrapper anymore, either
# much easier to read once you understand it!
def make_trie():
    return defaultdict(Trie)
trie = make_trie()
 
def insert(word):
    cur = trie
    for c in word:
        cur = cur[c]
    cur['#'] = True
    
def find(word):
    cur = trie
    for c in word:
        if c not in cur: return False
        cur = cur[c]
    return '#' in cur

Standard DSA Patterns

This used to include the leetcode cheatsheet, but it’s really just bloat of patterns in my opinion.

Union find / Disjoint Set Union

N = 1234
uf = list(range(N))
sz = [1] * N
 
def find(x):
    if uf[x] == x:
        return x
    uf[x] = find(uf[x])
    return uf[x]
    
def merge(a, b):
    a, b = find(a), find(b)
    if sz[a] > sz[b]:
        a, b = b, a
    # now sz[a] <= sz[b], we want smaller to go to bigger
    uf[b] = a
    sz[a] += b

Reversing a linked list

Explaining how to reverse a list is terrible, but writing the code is easy. You need to remember that you need two variables, and you start with a temporary one

class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        cur, prev = head, None
 
        while cur:
            temp = cur.next
            cur.next = prev
            prev = cur
            cur = temp
 
        return prev

Look at that pattern. We go temp → cur.net → prev → cur → temp. That is, every line ends with the start of the next line. From there it’s obvious.

We have to start with temp
What are we going to forget when we move forwards; what’s temp for? Ah, cur.next
What do we want cur.next to become? Ah, the previous
What do we want previous to become? Ah, the current,
Oh right we stored cur in the temp

It’s a bit cooked, but this method let me one-shot the problem even though I haven’t seen it in a year or thought about it for that long.

Boyer-Moore voting algorithm

This is for majority element. Its the obscure approach, and probably nobody will ask you this question while expecting this answer. It’s $O (n)$ with $O (1)$ space. I didn’t remember it at all while doing the problem.

class Solution:
    def majorityElement(self, nums):
        count = 0
        candidate = None
 
        for num in nums:
            if count == 0:
                candidate = num
            count += 1 if num == candidate else -1
 
        return candidate

This has the explanation. Quite funny, the opening paragraph simply says “If we had a way of counting instances of the majority element as $+ 1$ , and instances of other elements as $- 1$ , summing them would make it obvious that the majority element is indeed the majority element”. I guess the non-intuitive thing is that this still holds even when other numbers are mixed in. Say your first number is your target, then $l e n //2 - 1$ of the array is random numbers, and the remainder is the target. You’ll be initially good, then bad, then the number at the end will make it okay again.

zyros

Explorer

DSA 1 - Syntax and Snippets