Background
Given a directed acyclic graph, you want to find some order to place these elements such that for each node you visit, you’ve visited all the nodes that point towards it first. For instance, for this graph all three of or , or are valid topological orderings.
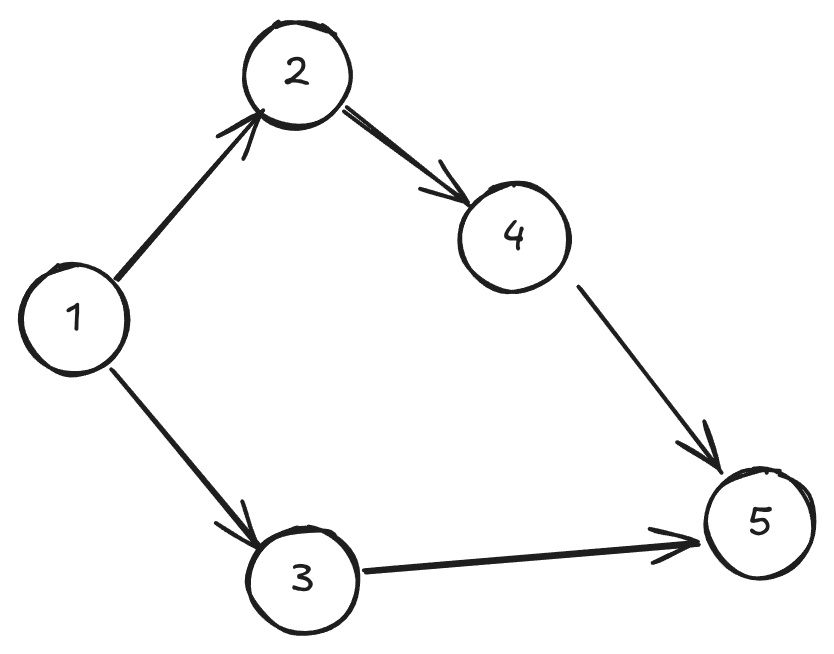
A common depiction is to place your nodes in a vertical view in this topological ordering, then place any extra edges along the sides. By the property of the topological sort, all these edges must point downwards and never upwards.

Method
There are two approaches to writing the code, and one of them is almost always a complexity trap. We can either strip away the leaves in a BFS-style approach, or we can do a DFS-style approach and pull the order out. Stripping the leaves sounds more intuitive, but ends up being harder to implement. You need to count the in-edges for each node and BFS by starting at the leaves (such as 1 in this graph) then decrementing each node as you go. When a node has zero in-edges, you add it to your topological sort. This is also known as Kahn’s Algorithm!
from collections import deque
from typing import List
# adj_list is an adjacency list, [[1, 2], [], []] means 0 -> 1, 0 -> 2
# N represents the number of nodes, and nodes are labelled 0 -> N - 1
def top_sort(adj_list: List[List[int]], N: int) -> List[int]:
in_degree = [0] * N
for items in adj_list:
for node in items:
in_degree[node] += 1
leaves = deque([i for i in range(N) if in_degree[i] == 0])
answer = []
while leaves:
leaf = leaves.popleft()
answer.append(leaf)
for node in adj_list[leaf]:
in_degree[node] -= 1
if in_degree[node] == 0:
leaves.append(node)
if len(answer) != N:
return [] # detected a cycle
return answerIn typing that out, I had to correct it several times… It’s easy to make an off-by-one, or a miscount somewhere with this. There are too many opportunities to subtract one too many, make your leaves still have in edges left over, and so on. Conceptually easier, but harder to execute during an interview.
For the “pulling it up” approach, you’re doing a DFS while skipping previously seen nodes, and when you exit a node you add it to your ordering list. So you’ll traverse down into the graph to the last node, add that node into your ordering, mark it as seen, then go back up.
For example in the below picture we start at 1, traverse down to the 5, then on the way up we mark them as seen and append to the list. We reach the 1 again (but we haven’t exited it!), then we traverse down the other neighbours and append them to the list as we exit. At the end we need to reverse the list.
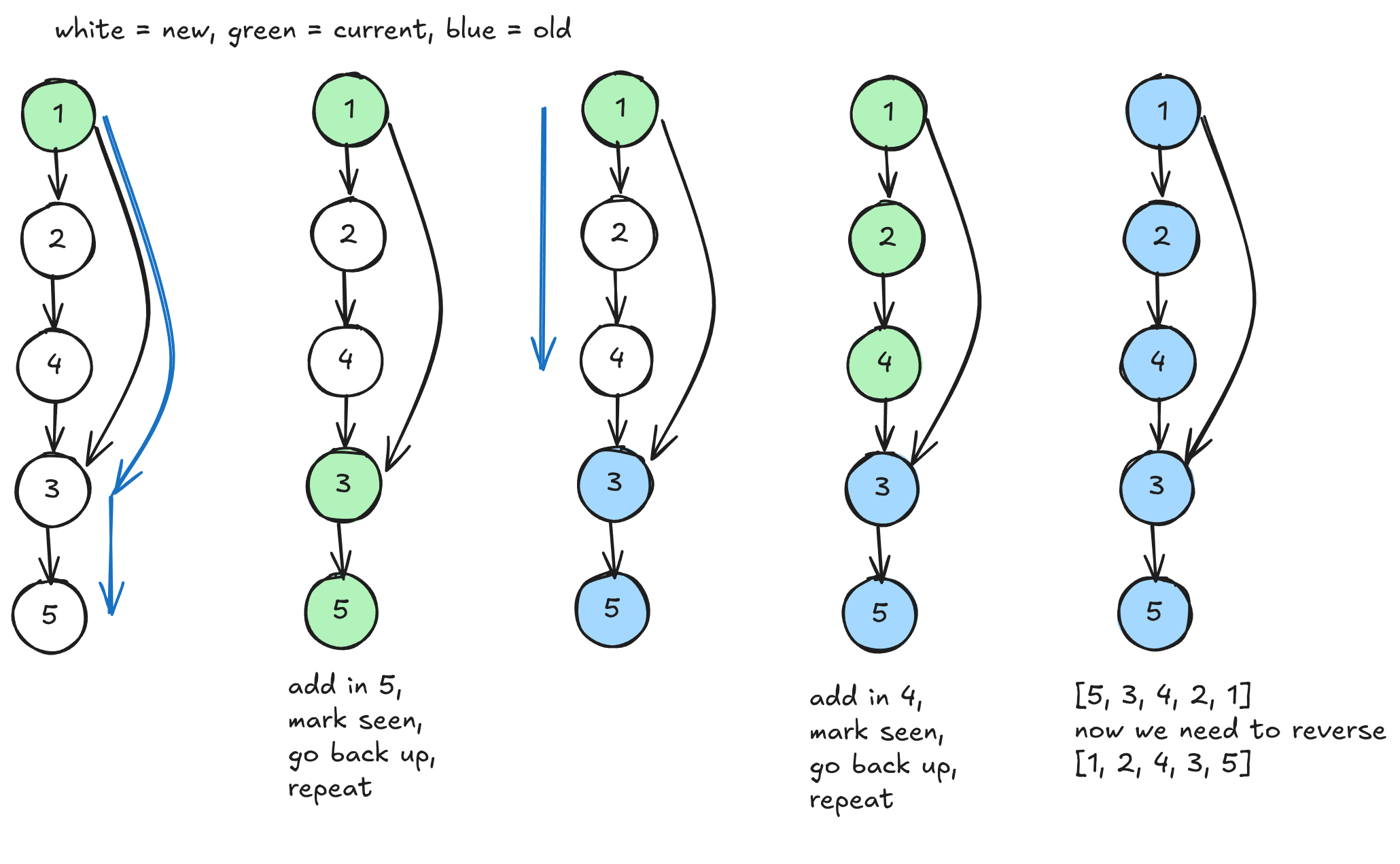
# DANGER
def top_sort_simple(adj_list: List[List[int]], N: int) -> List[int]:
seen = [False] * N
ordering = []
def dfs(node: int) -> None:
if seen[node]: return
seen[node] = True
for neigh in adj_list[node]:
dfs(neigh)
ordering.append(node)
for i in range(N):
if not seen[i]:
dfs(i)
return list(reversed(ordering))However, this approach has a cycle risk. If there is a cycle you’ll encounter a node twice within the same DFS and you’ll add it all the same into your result. To enable detection, you need to add a third state into your seen list which will represent the current cycle. In the above picture we already have this! The green nodes represented current nodes, so if we were to traverse into another green node, we’ve found a cycle!
def top_sort(adj_list: List[List[int]], N: int) -> List[int]:
NEW, CUR, OLD = 0, 1, 2
state = [NEW] * N
ordering = []
cycle = [False] # this is a list so we don't need nonlocal
def dfs(node: int) -> None:
if state[node] == CUR:
cycle[0] = True
return
if state[node] != NEW:
return
state[node] = CUR
for neigh in adj_list[node]:
dfs(neigh)
if cycle[0]: return
state[node] = OLD
ordering.append(node)
for i in range(N):
if state[i] == NEW:
dfs(i)
if cycle[0]: return []
return list(reversed(ordering))An upside of this approach is you can simplify it when you either don’t need the cycle detection, or you don’t need to return the order:
def is_cyclic(adj_list: List[List[int]], N: int) -> bool:
NEW, CUR, OLD = 0, 1, 2
state = defaultdict(int)
cycle = [False] # this is a list so we don't need nonlocal
def dfs(node: int) -> None:
if state[node] == CUR:
cycle[0] = True
return
if state[node] != NEW:
return
state[node] = CUR
for neigh in adj_list[node]:
dfs(neigh)
if cycle[0]: return
state[node] = OLD
for i in range(N):
if state[i] == NEW:
dfs(i)
if cycle[0]: return True
return FalseVariations
Most variations will be solveable with the stripping leaves approach, but the combinatoric problems can be easier with the pulling-up approach.
Defining layers
One issue is the topological sorts above can return multiple solutions. However, often times they want a specific ordering. For instance if you’re asked for a lexicographical order you’re forced to do this with Kahn’s. With Kahn’s, you can see each layer separately and clearly see the levels. So when you finish a level, you can sort it, then append it to the ordering. Alternatively, you can append this layer-by-layer, or determine whether the topological sort is unique.
from collections import deque
from typing import List
def top_sort_layers(adj_list: List[List[int]], N: int) -> List[List[int]]:
in_degree = [0] * N
for items in adj_list:
for node in items:
in_degree[node] += 1
leaves = deque([i for i in range(N) if in_degree[i] == 0])
answer = []
nodes_processed = 0
while leaves:
sz = len(leaves)
# Here you can handle one layer at a time
answer.append(list(leaves))
for _ in range(sz):
leaf = leaves.popleft()
nodes_processed += 1
for node in adj_list[leaf]:
in_degree[node] -= 1
if in_degree[node] == 0:
leaves.append(node)
if nodes_processed != N:
return [] # Cycle detected
return answerCritical path
To find the critical path (the longest path in the top sort) you just need to store how deep each node is in the path,
def longest_path_dfs(adj_list: List[List[int]], N: int) -> int:
NEW, CUR, OLD = 0, 1, 2
state = [NEW] * N
dist = [0] * N
def dfs(node: int) -> int:
if state[node] == CUR:
return -1
if state[node] == OLD:
return dist[node]
state[node] = CUR
max_child_dist = 0
for neigh in adj_list[node]:
child_dist = dfs(neigh)
if child_dist == -1:
return -1
max_child_dist = max(max_child_dist, child_dist)
dist[node] = 1 + max_child_dist
state[node] = OLD
return dist[node]
overall_max = 0
for i in range(N):
if state[i] == NEW:
val = dfs(i)
if val == -1:
return -1
overall_max = max(overall_max, val)
return overall_maxReturning cycle
If you maintain a parent lookup for each node you can introduce more tricks. For instance, to print a cycle, you can do the pull-it-up approach but when you hit a cycle you can traverse back up.
from typing import List, Optional
def find_and_print_cycle(adj_list: List[List[int]], N: int) -> List[int]:
NEW, CUR, OLD = 0, 1, 2
state = [NEW] * N
# To reconstruct the path
parent_map: dict[int, int] = {}
cycle_path: List[int] = []
def dfs(node: int) -> bool:
state[node] = CUR
for neigh in adj_list[node]:
if state[neigh] == CUR:
curr = node
path = [curr]
while curr != neigh:
curr = parent_map[curr]
path.append(curr)
path.append(node) # Close the loop
cycle_path[:] = list(reversed(path))
return True
if state[neigh] == NEW:
parent_map[neigh] = node
if dfs(neigh):
return True
state[node] = OLD
return False
for i in range(N):
if state[i] == NEW:
if dfs(i):
return cycle_path
return [] # No cycleAll possible paths
For all possible paths, the implementation can be a bit weird. Since the time complexity is going to be very high anyways with creating all the lists, you may as well iterate by checking the state of each node every iteration since it simplifies it. So you end up with a Kahn’s algorithm but you don’t need the queue.
def all_top_sorts(adj_list: List[List[int]], N: int) -> List[List[int]]:
in_degree = [0] * N
for neighbors in adj_list:
for node in neighbors:
in_degree[node] += 1
visited = [False] * N
results: List[List[int]] = []
def backtrack(path: List[int]) -> None:
if len(path) == N:
results.append(list(path))
return
for i in range(N):
if not visited[i] and in_degree[i] == 0:
visited[i] = True
path.append(i)
for neighbor in adj_list[i]:
in_degree[neighbor] -= 1
backtrack(path)
visited[i] = False
path.pop()
for neighbor in adj_list[i]:
in_degree[neighbor] += 1
backtrack([])
return resultsConclusion
In this article we went over what a topological sort is, the two fundamental approaches, and a number of variations. Topological sort problems are not always obvious, particularly when it is not clear the problem state is actually a graph. They tend to be useful in problems that require an ordering of some kind.
 zyros
zyros